Паркеты - геометрия и искусство
Главное меню:
Лайфхак для парней: как добавить 💰 своей девушке?
Находка для тех, чьи девушки и супруги работают в сфере услуг: маникюр, брови, ресницы и так далее
🤔 Вы же наверняка задумывались, как помочь своей половинке зарабатывать больше? Но что делать, если во всех этих маркетингах и процедурах не разбираешься от слова «совсем»? Мы нашли выход — это сервис VisitTime
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
А еще там первый месяц бесплатно, поэтому лучшее, что вы можете сделать сейчас — установить или показать его своей принцессе Всё интуитивно понятно и просто, достаточно нажать на этот текст и запустить чат-бота
Паркеты
Паркет — натуральное деревянное напольное покрытие.
Зарождением паркета мир обязан готической Европе, где в тот период (в конце 13 — начале 14 столетий) в домах вельможной знати полы стали выстилаться оригинально подобранными дощечками из различных пород деревьев, которые формировали невообразимо красивые на то время напольные покрытия в форме рисунков и орнаментов (история паркета здесь).
Паркет (замощение) - специальный случай орнамента.
Замощение - разбиение плоскости или пространства на фигуры без общих внутренних точек.
Паркеты бывают правильными, полуправильными, неправильными.
Геометрические паркеты
Паркет (или мозаика) - бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек; но мы будем рассматривать как правильные, так и неправильные многоугольники.
Итак, какими же многоугольниками можно замостить плоскость?
Паркеты из одинаковых правильных многоугольников
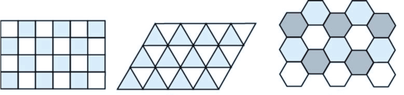
Сумма всех углов n-угольника равна 180°(n-2). Все углы правильного многоугольника равны; следовательно, каждый из них равен 180°(n-2)/n. В каждой вершине паркета сходится целое число углов; поэтому число 2·180° должно быть целым кратным числа 180°(n-2)/n. Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников. Общие углы в сумме должны давать 360° .
Не существует правильных паркетов из семиугольников, восьимиугольников и т.д.
Посмотри, как цвета влияют на восприятие треугольного паркета и образовывают узор из других фигур
Паркеты из разных правильных многоугольников (полуправильные)
Сначала выясним, какое количество различных правильных многоугольников (с одинаковыми длинами сторон) может находиться вокруг каждой точки. Величина угла правильного многоугольника должна находиться в интервале от 60° до 180° (не включая); следовательно, число многоугольников, находящихся в окрестности точки, должно быть больше 2 (360°/180°) и не может превышать 6 (360°/60°).
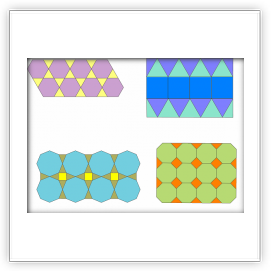
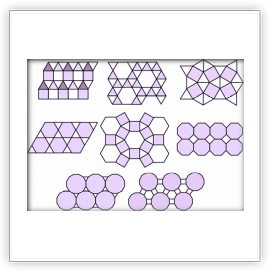
Можно показать, что существуют следующие способы уложить паркет комбинациями правильных многоугольников: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) - два варианта паркета; (3,4,4,6) - четыре варианта; (3,3,3,4,4) - четыре варианта; (3,3,3,3,6); (3,3,3,3,3,3) (цифры в скобках - обозначения многоугольников, сходящихся в каждой вершине: 3 - правильный треугольник, 4 - квадрат, 6 - правильный шестиугольник, 12 - правильный двенадцатиугольник).
Паркеты из квадратов разных размеров
Замощение плоскости может быть произведено не только многоугольниками, но и фигурами более сложного вида. (см. Эшер)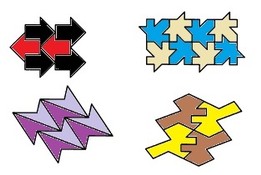
Все выше перечисленные паркеты периодичны, в каждом можно выделить область из нескольких фигур, из которой параллельными сдвигами получается весь паркет.
Существуют и непериодические замощения: спиральное замощение девятиугольниками, придуманное немецким математиком Х. Фодербергом (1936), паркет английского математика Роджера Пенроуза.