Мозаики Пенроуза - геометрия и искусство
Главное меню:
🤔 Вы же наверняка задумывались, как помочь своей половинке зарабатывать больше? Но что делать, если во всех этих маркетингах и процедурах не разбираешься от слова «совсем»? Мы нашли выход — это сервис VisitTime
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
А еще там первый месяц бесплатно, поэтому лучшее, что вы можете сделать сейчас — установить или показать его своей принцессе Всё интуитивно понятно и просто, достаточно нажать на этот текст и запустить чат-бота
Мозаики Пенроуза
Мозаика Пенроуза, плитки Пенроуза — непериодическое разбиение плоскости, апериодические регулярные структуры, замощение плоскости ромбами двух типов — с углами 72° и 108° («толстые ромбы») и 36° и 144° («тонкие ромбы»), такими (подчиняются пропорции «золотого сечения»), что любые два соседних (то есть имеющих общую сторону) ромба не образуют вместе параллелограмм. Названа в честь Роджера Пенроуза, интересовавшегося проблемой «замощения», то есть заполнения плоскости фигурами одной формы без зазоров и перекрываний.
Все такие замощения непериодичны и локально изоморфны друг другу (то есть любой конечный фрагмент одной мозаики Пенроуза встречается в любой другой). «Самоподобие» — можно так объединить соседние плитки мозаики, чтобы снова получилась мозаика Пенроуза.
Несколько отрезков можно нарисовать на каждой из двух плиток так, что при выкладывании мозаики концы этих отрезков совместятся и на плоскости образуются несколько семейств параллельных прямых линий (полосы Аммана).
Расстояния между соседними параллельными прямыми принимают ровно два различных значения (а для каждого семейства параллельных прямых последовательность этих значений обладает самоподобием).
Мозаики Пенроуза, имеющие дыры, покрывают всю плоскость, за исключением фигуры конечной площади. Увеличить дыру, сняв несколько (конечное число) плиток, после чего замостить непокрытую часть полностью, нельзя.
Задача решается замощением фигурами, создающими периодически повторяющийся рисунок, но Пенроуз хотел отыскать именно такую фигуру, которая при замощении плоскости не создавала бы повторяющихся узоров. Считалось, что нет таких плиток, из которых строились бы только непериодические мозаики. Пенроуз подбирал множество плиток различной формы, в итоге их оказалось только 2, имеющих «золотое сечение», которое лежит в основе всех гармоничных соотношений. Это фигуры ромбовидной формы с углами 108° и 72°. Позже фигуры упростились до формы просто ромба (36° и 144°), в основе лежит принцип «золотого треугольника».
Получившиеся узоры имеют квазикристаллическую форму, которая имеет осевую симметрию 5-го порядка. Структура мозаики связана с последовательностью Фибоначчи.
(Википедия)
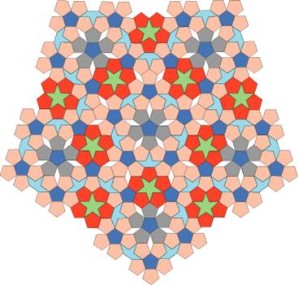
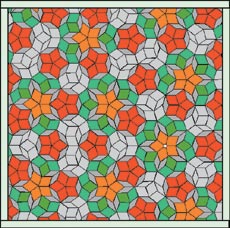
Мозаика Пенроуза. Белой точкой отмечен центр поворотной симметрии 5-го порядка: поворот вокруг нее на 72° переводит мозаику саму в себя.
