Окружность и круг - геометрия и искусство
Главное меню:
Лайфхак для парней: как добавить 💰 своей девушке?
Находка для тех, чьи девушки и супруги работают в сфере услуг: маникюр, брови, ресницы и так далее
🤔 Вы же наверняка задумывались, как помочь своей половинке зарабатывать больше? Но что делать, если во всех этих маркетингах и процедурах не разбираешься от слова «совсем»? Мы нашли выход — это сервис VisitTime
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
А еще там первый месяц бесплатно, поэтому лучшее, что вы можете сделать сейчас — установить или показать его своей принцессе Всё интуитивно понятно и просто, достаточно нажать на этот текст и запустить чат-бота
Окружность и круг
Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)
Круг – это часть плоскости, ограниченная окружностью.Точка О также называется центром круга.
Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.
Посмотрите, как используется круг и окружность в нашей жизни, искусстве, дизайне.
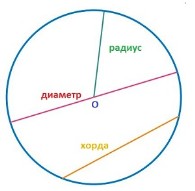
Хорда - греческое - струна, стягивающая что-то
Диаметр - "измерение через"
КРУГЛАЯ ФОРМА
Углы могут встречаться во все более возрастающем количестве, приобретать, соответственно, все больший разворот – пока не исчезнут окончательно и плоскость не станет кругом. Это очень простой и одновременно очень сложный случай, о котором мне хотелось бы поговорить подробно. Здесь необходимо отметить, что как простота, так и сложность обусловлены отсутствием углов. Круг прост, поскольку давление его границ, в сравнении с прямоугольными формами, нивелировано – различия здесь не так велики. Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.
В. Кандинский
В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.
В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.
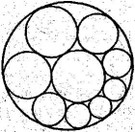
На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке. Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности. Отсюда следует, что если однажды цепочка не замкнулась, то она не замкнется при любом выборе третьей окружности. Художнику, рисовавшему изображенную цепочку, пришлось бы немало потрудиться, чтобы она получилась, или обратиться к математику для расчета расположения двух первых окружностей, при котором цепочка замыкается.
Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна - катки для перевозки тяжестей.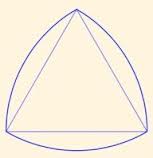 
А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.
Энц. "Я познаю мир. Математика", 2006
У каждого треугольника имеется, и притом единственная, окружность девяти точек. Это окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника : основания его высот D1 D2 и D3, основания его медиан D4, D5 и D6 середины D7, D8 и D9 отрезков прямых от точки пересечения его высот Н до его вершин.
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха).
Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это -точки ее касания с четырьмя окружностями специального вида. Одна из этих окружностей вписанная, остальные три - вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек D10, D11, D12 и D13 называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек.
Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой Н- его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.
Энц. справочник юного математика, 1989