Треугольники - геометрия и искусство
Главное меню:
Лайфхак для парней: как добавить 💰 своей девушке?
Находка для тех, чьи девушки и супруги работают в сфере услуг: маникюр, брови, ресницы и так далее
🤔 Вы же наверняка задумывались, как помочь своей половинке зарабатывать больше? Но что делать, если во всех этих маркетингах и процедурах не разбираешься от слова «совсем»? Мы нашли выход — это сервис VisitTime
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
А еще там первый месяц бесплатно, поэтому лучшее, что вы можете сделать сейчас — установить или показать его своей принцессе Всё интуитивно понятно и просто, достаточно нажать на этот текст и запустить чат-бота
Треугольники
Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.
Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.
Вершины — три точки А, В и С. Стороны — отрезки АВ, ВС и СА.
Углы — ∟ ВАС, ∟ СВА и ∟ АСВ.
Периметр треугольника — сумма длин трех сторон треугольника.
Медиана треугольника (m)— отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника (b) — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника (h)— перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.
Теорема. Сумма углов треугольника 180°
Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон.
АВ <АС + СВ.
АС <AB + BC.
BC <ВА + АС.
В треугольнике:
1) против большей стороны лежит больший угол
2) против большего угла лежит большая сторона
В прямоугольном треугольнике гипотенуза больше катета
Классификация треугольников
По углам
В треугольнике может быть только один тупой угол
В треугольнике может быть только один прямой угол
По сторонам
Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
Теорема
В равнобедренном треугольнике углы при основании равны.
Теорема
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Равносторонний треугольник — все стороны и углы равны
Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
В равных треугольниках против соответственно равных сторон лежат равные углы.
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Прямоугольный треугольник
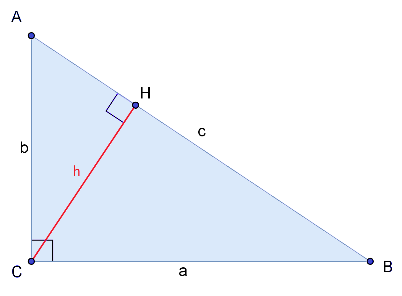
ГИПОТЕНУЗА - сторона прямоугольного треугольника, лежащая прготив прямого угла. (греческое "гипо" - под, снизу, внизу, "тейнейн" - натягивать (тетеву лука)).
КАТЕТ — одна из двух сторон прямоугольного треугольника, образующих прямой угол. Название «катет» происходит от греческого káthetos — перпендикуляр, опущенный, отвесный. Название также встречается в архитектуре и означает отвес через средину задка ионической капители.
СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
• Сумма двух острых углов прямоугольного треугольника равна 90°.
• Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету
Треугольник — это простейшая фигура: три стороны и три вершины. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы.
Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).
Через 2000 лет в Древней Греции изучение свойств треугольника ведется очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как меридианы и высоты, пересекаются в одной точке.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения, лежат, на одной окружности». Эта окружность получила название «окружности девяти точек». Ее центр оказался в се-редине отрезка, соединяющего точку пересечения высот с центром описанной окружности.
Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывает такую красивую, с теорему: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник называется внешним треугольником Наполеона. " Аналогично строится и внутренний треугольник Наполеона.
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все. 
Тем удивительнее было открытие, сделанное американским математиком Франком Морли. Он доказал, что если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника (1899).
Энц. "Я познаю мир. Математика", 2006
Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского.
