Четырёхугольник - геометрия и искусство
Главное меню:
Лайфхак для парней: как добавить 💰 своей девушке?
Находка для тех, чьи девушки и супруги работают в сфере услуг: маникюр, брови, ресницы и так далее
🤔 Вы же наверняка задумывались, как помочь своей половинке зарабатывать больше? Но что делать, если во всех этих маркетингах и процедурах не разбираешься от слова «совсем»? Мы нашли выход — это сервис VisitTime
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
А еще там первый месяц бесплатно, поэтому лучшее, что вы можете сделать сейчас — установить или показать его своей принцессе Всё интуитивно понятно и просто, достаточно нажать на этот текст и запустить чат-бота
Четырёхугольник
ЧЕТЫРЕХУГОЛЬНИК
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали. Две несмежные стороны называются противоположными. Две вершины, не являющиеся соседними, также называются противоположными.
Сумма углов выпуклого четырехугольника равна 360°.
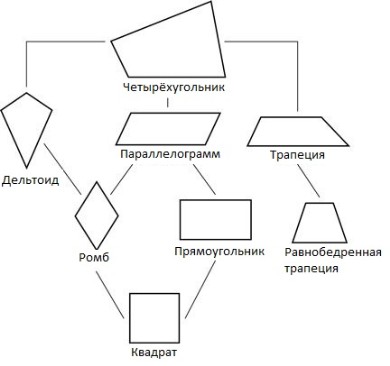
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.
Сол ле Витт
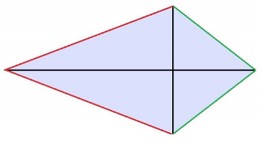Дельтоид — четырёхугольник, обладающий двумя парами сторон одинаковой длины. В отличие от параллелограмма, равными являются не противоположные, а две пары смежных сторон. Выпуклый дельтоид имеет форму, похожую на воздушного змея.
Углы между сторонами неравной длины равны.
Диагонали дельтоида (или их продолжения) пересекаются под прямым углом.
В любой выпуклый дельтоид можно вписать окружность, кроме этого, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон. Для невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.
Если угол между неравными сторонами дельтоида прямой, то вокруг него можно описать окружность (вписанный дельтоид).
Если пара противоположных сторон дельтоида равны, то такой дельтоид является ромбом.
Если пара противоположных сторон и обе диагонали дельтоида равны, то дельтоид является квадратом. Квадратом является и вписанный дельтоид с равными диагоналями.
Четырехугольники: невыпуклый и с самопересечением