правильные - геометрия и искусство
Главное меню:
правильные
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры); воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры); в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.
Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал. Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке. Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра. В 18-м предложении утверждается, что не существует других правильных многогранников. Андреас Шпейзер отстаивал точку зрения, что построение пяти правильных многогранников является главной целью дедуктивной системы геометрии в том виде, как та была создана греками и канонизирована в «Началах» Евклида. Большое количество информации XIII книги «Начал», возможно, взято из трудов Теэтета.
/википедия/
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Пифагорейская школа (VI—V вв. до н. э. )
Для обоснования своих философских теорий пифагорейцы использовали правильные многогранники, формы которых придавали элементам первооснов бытия, а именно:
огонь — тетраэдр (его гранями являются четыре правильных треугольника);
земля — гексаэдр (куб — многогранник, гранями которого являются шесть квадратов);
воздух — октаэдр (его гранями являются восемь правильных треугольников);
вода — икосаэдр (его гранями являются двадцать правильных треугольников);
вся Вселенная, по мнению древних, имела форму додекаэдра (егс гранями являются двенадцать правильных пятиугольников).
Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: «Тетра» — четыре; «Гекса» — шесть; «Окто» — восемь: «Икоси» — двадцать;«Додека» — двенадцать; «Эдра» — грань.
Наиболее простым таким правильным многогранником является треугольная пирамида, грани которой правильные треугольники. В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник. Иногда тетраэдром называют также произвольную треугольную пирамиду.
Многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится четыре грани - называется октаэдром.
Многогранник, в каждой вершине которого сходится пять правиль ных треугольников, поверхность из двадцати правильных треугольников- называется икосаэдром.
Кроме куба других правильных многогранников, гранями которых являются квадраты, не существует. Куб имеет шесть граней, и поэтому называется также гексаэдром.
Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится три грани, поверхность из двенадцати правильных пятиугольников, - называется додекаэдром.
Таким образом, имеется только пять правильных многогранников: правильный тетраэдр, гексаэдр (куб), октаэдр, додекаэдр и икосаэдр.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе

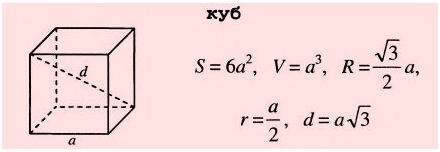



В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы, архитекторы, художники.
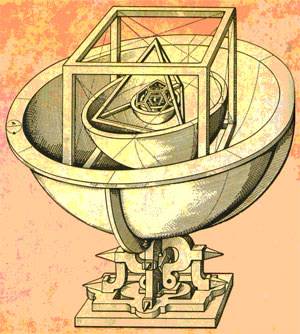
Иоганн Кеплер (1571—1630) в своей работе «Тайна мироздания» в 1596 году, используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Геометрия Солнечной системы, по Кеплеру, заключалась в следующем: «Земля (имеется в виду орбита Земли) есть мера всех орбит. Вокруг нее опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфер Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг куба сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в нег сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная него сфера есть сфера Меркурия». Такая модель Солнечной системы получила название «Космического кубка» Кеплера.
Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера-Пуансо).
