Построение - геометрия и искусство
Главное меню:
Лайфхак для парней: как добавить 💰 своей девушке?
Находка для тех, чьи девушки и супруги работают в сфере услуг: маникюр, брови, ресницы и так далее
🤔 Вы же наверняка задумывались, как помочь своей половинке зарабатывать больше? Но что делать, если во всех этих маркетингах и процедурах не разбираешься от слова «совсем»? Мы нашли выход — это сервис VisitTime
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
А еще там первый месяц бесплатно, поэтому лучшее, что вы можете сделать сейчас — установить или показать его своей принцессе Всё интуитивно понятно и просто, достаточно нажать на этот текст и запустить чат-бота
Построение
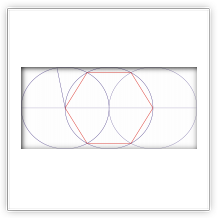
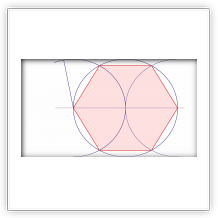
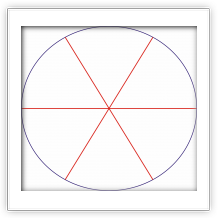
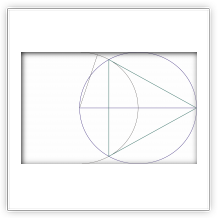
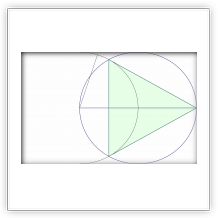
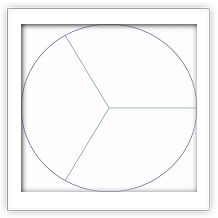
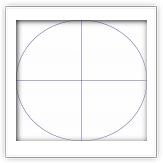
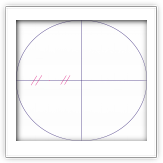
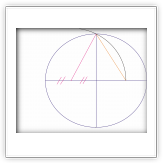
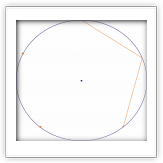
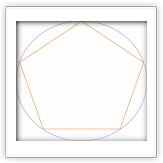
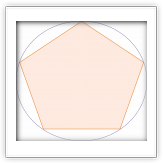
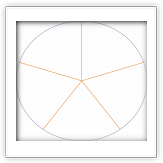
Построение правильного многоугольника с n сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на n равных частей, так как соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.
Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для n = 3, 4, 5, 6, 15. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки.
На сегодняшний день известны следующие простые числа Ферма: 3, 5, 17, 257, 65537. Вопрос о наличии или отсутствии других таких чисел остаётся открытым.
Правильный шестиугольник
Правильный треугольник
правильный пятиугольник
