Точки и прямые - геометрия и искусство
Главное меню:
Точки и прямые
В 1953 году я понял, что прямая линия ведёт человечество к упадку. Тирания прямой стала абсолютной. Прямая линия - это нечто трусливое, прочерченное по линейке, без эмоций и размыщлений; это линия, не существующая в природе. И на этом насквозь прогнившем фундаменте построена наша обречённая цивилизация.
/Ф. Хундертвассер/
Основные геометрические понятия возникли еще в доисторические времена. Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий. Одним из первых достижений абстрактного мышления древнего человека стало понимание прямой линии.
Точки (пункты) на геометрических чертежах и рисунках обозначают прописными буквами латинского алфавита, а прямые — строчными.
Следует напомнить, что линия будь то прямая или кривая состоит из бесчисленного множества точек. Поэтому справедливы выражения: «Точка А лежит на прямой l » или «прямая l проходит через точку В».
Прямая бесконечна. Однако на рисунках мы изображаем лишь часть прямой, при этом не забываем, что она бесконечна.
Прямая не проходит через точку, если точка не принадлежит ей.
Пряма́я — одно из фундаментальных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой).
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
К основным свойствам прямой относятся:
Черед две различные точки проходит одна единственная прямая. Следовательно две прямые не могут иметь более одной общей точки.
Две разные прямые, имеющие общую точку, пересекаются в ней. В связи с тем, что две точки определяют прямую, проходящую через них, прямую обозначают сочетанием букв, к примеру, прямая АВ, прямая PQ.
Точка М, лежащая на прямой а, разбивает её на две части. Каждая из которых называется полупрямой или лучом. Точка М служит началом каждого их этих лучей. Две точки М и N разбивают прямую на три части: два луча МР и NQ и отрезок MN.
Прямая разбивает плоскость на 2 части. Часть плоскости лежащая по одну сторону от этой прямой, называется полуплоскостью.
Если прямые не имеют общих точек, говорят, что они параллельны.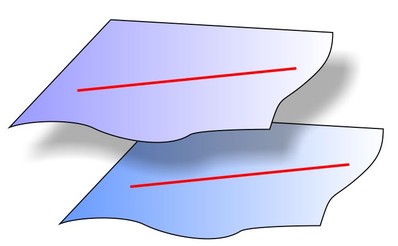
Если две прямые имеют одну общую точку, говорят, что они пересекаются в этой точке.
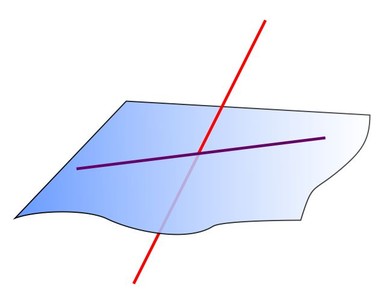
Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.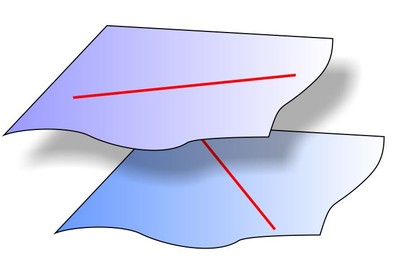
Пример скрещивающихся прямых
