Золотое сечение - геометрия и искусство
Главное меню:
Золотое сечение
Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое – деление отрезка в среднем и крайнем отношении.
И. Кеплер
Деление отрезка в среднем и крайнем отношении часто использовалось в искусстве, встречается оно и в живой природе, что дало повод математику XVI в., другу известного художника Леонардо да Винчи, монаху Луке Пачоли назвать такое деление отрезка божественной, великолепной пропорцией. По поводу этой пропорции он употребляет много слов, но в истории утвердились два варианта: золотая пропорция, или золотое сечение.
Эта наша пропорция, высокочтимый герцог, достойна такой привелегии и такого превосходства, какие только можно высказать по поводу её безграничных возможностей, поскольку, не зная её, никогда нельзя обнаружить ни в философии, ни в другой какой-нибудь науке очень многих вещей, достойных восхищения.
Л. Пачоли
Коль скоро, стало быть, все вещи прекрасны и в известном смысле могут служить источником наслаждения, а красоты и наслаждения нет без пропорциональности, пропорциональность же прежде всего существует в числах, необходимо, чтобы всё поддавалось счислению, отчего число и есть в духе важнейший прообраз создателя, а в вещах - важнейший след, ведущий к мудрости.
Д. Бонавентура
Золотое сечение называют гармонической пропорцией.
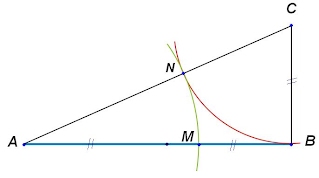
Построить золотое сечение можно пользуясь следующими указаниями:
Построить отрезок АВ
В точке В восставить перпендикуляр к АВ
Разделить АВ пополам
Отложить на перпендикуляре точку C так, чтобы ВC= 1/2 АВ
Соединить точки А и C
Отложить CN=ВC
Отложить АM=АN.
Точка М является искомой, она производит золотое сечение отрезка
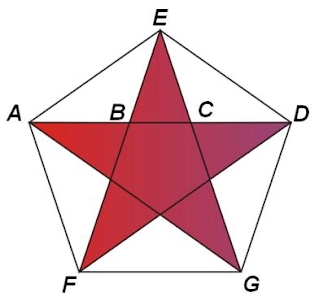
Замечательный пример «золотого сечения» представляет собой пятиугольник – выпуклый и звёздчатый. Звёздчатый пятиугольник называется пентаграммой («пенте» - пять). Он служит символом Пифагорейского союза.
В этой фигуре наблюдается удивительное постоянство отношений отрезков: AD:AC = AC:CD = AB:BC = AD:AE = AE:EC
«ЗОЛОТАЯ» ПРОПОРЦИЯ
То, что части красиво сложенного человеческого тела находятся в определенной пропорции, знает каждый: недаром мы говорим о пропорционально сложенной фигуре. Но далеко не всём известно, что здесь имеет место золотое деление. Лучшим примером того, что древние ваятели использовали этот принцип при изображении человеческого тела, являются античные статуи. Идеально сложенное человеческое тело полностью отвечает этому принципу. Если высоту хорошо сложенной фигуры разделить в крайнем и среднем отношении, то линия раздела окажется на высоте талии. Особенно хорошо удовлетворяет этому закону мужская фигура. Любая античная скульптура отвечает закону золотой пропорции. Каждую отдельно взятую часть тела (голову, руку, кисть) также можно разделить на естественные части по закону золотого сечения.
Рука согласно принципу «золотого» сечения распадается на «свои анатомические части» - плечо, предплечье, кисть. Разделение кисти руки, лица отвечает тоже этому принципу.
«Золотая» пропорция - понятие математическое. Но она явля ется критерием гармонии и красоты, а это уже категории искусства.
В книгах о «золотом сечении» можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими «золотое» сечение, то с других точек зрения они будут выглядеть иначе. «Золотое» сечение дает наиболее спокойное соотношение размеров тех или иных длин.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н.э.) - храм Афины.
Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали и находили в соотношениях его частей «золотую» пропорцию. Тщательные измерения Парфенона показали, что в нем нет прямых линий, а поверхности не плоские, а слегка изогнутые. Зодчие Греции знали, что строго горизонтальная линия и плоская поверхность наблюдателю издалека представляются прогнувшимися в середине.
Другим примером использования «золотой» пропорции из архитектуры древности является Пантеон.
Скульптурные сооружения, памятники, воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиг и деяния. Пропорции «золотого сечения» создают впечатления гармонии, красоты, поэтому скульптуры использовали их в своих произведениях. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.
Великий древнегреческий скульптор Фидий часто использовал «золотое» сечение в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (который считается одним из чудес света) и Афины Парфенос.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе




Принято считать, что использование золотого прямоугольника в живописи придает полотну гармонию и умиротворенность. В произведении Леонардо да Винчи «Тайная вечеря» можно увидеть золотой прямоугольник, здесь соотношение сторон картины близко к числу Ф.

С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
Статья из журнала "Наука и жизнь"
http://www.nkj.ru/archive/articles/3070/?sphrase_id=82234
Группа "Золотое сечение" (группа Пюто)
Группа Пюто образовалась в 1910 году, в результате постоянных встреч художников на квартире у живописца Жака Вийона, где обсуждалось творчество таких мастеров-кубистов, как П.Пикассо и Ж.Брак. Название группы по городку Пюто было выбрано умышленно, чтобы отделить свои работы от созданий Пикассо и Брака. В то же время члены этого объединения, находясь под сильным влиянием новаторства их работ, разработали несколько теорий, научно обосновывающих эстетику и гармоничность кубизма. Члены группы Пюто интересовались также африканским традиционным искусством, футуризмом, художественной фотографией.
В 1912 году художник Марсель Дюшан представляет группе свою новую работу, полотно Ню, спускающаяся по лестнице № 2. В настоящее время эта картина считается одной из эпохальных для начала ХХ века, открывшая искусству мир футуризма.
В 1912 году часть художников из группы Пюто образовали сообщество по организации выставок — Золотое сечение.
