Фракталы - геометрия и искусство

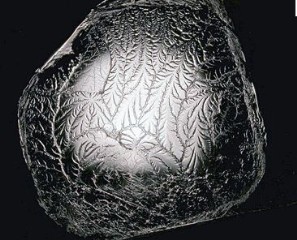
Морозные узоры на окне, замысловатая и неповторимая форма снежинок, сверкающие молнии в ночном небе завораживают и пленяют своей необыкновенной красотой. Однако мало кто знает, что все это является сложными фрактальными структурами.

Бесконечно самоподобные фигуры, каждый фрагмент которых повторяется при уменьшении масштаба, называются фракталами. Сосудистая система человека, система альвеол животного, извилины морских берегов, облака в небе, контуры деревьев, антенны на крышах домов, клеточная мембрана и звездные галактики — все это удивительное порождение хаотического движения мира есть фракталы.

Первые образцы самоподобных множеств с необычными свойствами появились в XIX веке. Термин «фракталы», который происходит от латинского слова «fractus» — дробный, ломанный, был введен Бенуа Мандельбротом в 1975 году. Таким образом, фрактал представляет собой структуру, состоящую из частей, подобных целому. Именно свойство самоподобия резко отличает фракталы от объектов классической геометрии.

Множество Жюлиа (в честь французского математика Гастона Жюлиа (1893-1978), который вместе с Пьером Фату первым занаялся изучением фракталов. В 1970-х годах его работы популяризировал Бенуа Мандельброт)

Геометрические фракталы

История фракталов в XIX веке началось именно с изучения геометрических фракталов. Фракталы ярко отражают свойство самоподобия. Наиболее наглядными примерами геометрических фракталов являются:

Кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины. Эта кривая не имеет касательной ни в одной точке.
Множество Кантора — неплотное несчётное совершенное множество.
Губка Менгера — это аналог множества Кантора с тем лишь отличием, что построен этот фрактал в трехмерном пространстве.
Треугольник или ковер Серпинского также является аналогом множества Кантора на плоскоти.
Фракталы Вейерштрасса и Ван дер Вардена представляют собой недифференцируемую непрерывную функцию.
Траектория броуновский частицы также не дифференцируема.
Кривая Пеано — это непрерывная кривая, которая проходит через все точки квадрата.
Дерево Пифагора.

Рассмотрим триадную кривую Коха.
Для построение кривой существует простая рекурсивная процедура образования фракта кривых на плоскости. В первую очередь необходимо задать произвольную ломаную с конечным числом звеньев, так называемым генератором. Далее каждое звено заменяется образующим элементом, точнее ломаной, подобной генератору. В результате такой замены образуется новое поколение кривой Коха. В первом поколении кривая состоит из четырех прямолинейных звеньев, длина каждого из которых равна 1/3. Чтобы получить третье поколение кривой выполняют тот же алгоритм — каждое звено заменяется на уменьшенный образующий элемент. Таким образом, для получения каждого последующего поколения, все звенья предыдущего заменяются уменьшенным образующим элементов. Тогда, кривая n-го поколения при любом конечном n называется предфракталом. В случае, когда n стремится к бесконечности кривая Коха становится фрактальным объектом.

Обратимся к другому способу построения фрактального объекта. Для его создания необходимо изменить правила построение: пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменяем единичный отрезок на образующий элемент таким образом, чтобы угол был сверху. То есть, при такой замене происходит смещение середины звена. Последующие поколения строятся по правилу: первое слева звено заменяется на образующий элемент тким образом, чтобы середина звена смещалась влево от направления движения. Далее замена звеньев чередуется. Предельная фрактальная кривая, построенная по такому правилу, называется драконом Хартера-Хейтуэя.

В компьютерной графике геометрические фраткалы используются для моделирования изображений деревьев, кустов, горных массивов, береговой линии. Двухмерные геометрические фракталы широко используются для создания объемных текстур.

Бенуа́ Мандельбро́т (1924-2010) — французский и американский математик, создатель фрактальной геометрии. Лауреат премии Вольфа по физике (1993).

Бенуа Мандельброт родился в Варшаве в 1924 году. В 1936 году вся семья эмигрировала во Францию и поселилась в Париже. Здесь Мандельброт попал под влияние своего дяди Шолема Мандельбройта, известного парижского математика, члена группы математиков, известной под общим псевдонимом Николя Бурбаки.

У Бенуа открылся необычный математический дар, который позволил ему сразу после войны стать студентом Политехнической школы Парижа. Оказалось, что у Бенуа великолепное пространственное воображение. Даже алгебраические задачи он решал геометрическим способом. Оригинальность его решений позволила ему поступить в университет.

Окончив университет, Мандельброт переехал в США, где окончил Калифорнийский технологический институт. По возвращении во Францию, он получил докторскую степень в Университете Парижа в 1952 году. В 1958 году Мандельброт окончательно поселился в США, где приступил к работе в научно-исследовательском центре IBM в Йорктауне. Он работал в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики.

Фракта́л (лат. fractus — дроблёный) — термин, введённый Бенуа Мандельбротом в 1975 году. До сих пор нет строгого математического определения фрактальных множеств.  Он смог обобщить и систематезировать «неприятные» множества и построить красивую и интуитивно понятную теорию. Он открыл удивительный мир фракталов, красота и глубина которых порой поражают воображение, вызывают восторг у ученых, хужожников, философов… Работа Мандельброта была стимулирована передовыми компьютерными технологиями, которые позволили генерировать, визуализировать и исследовать различные множества.